
L’évaluation est une science
Bien souvent, on s'apprête à prendre des décisions qui pourront déterminer les études ou bien la carrière de certains. Ne pas se poser la question de la fiabilité de la mesure est une faute morale envers les intéressés, et une erreur pour l’institution elle-même, qui ne portera pas le jugement approprié, qui ne prendra pas les décisions pertinentes.
Nous verrons dans cet article que la qualité de la mesure issue d’une évaluation peut se calculer de manière tout à fait précise. En conclusion, nous verrons qu’une évaluation qui n’inclurait que 10 questions ne peut pas apporter des résultats utilisables. Nous verrons qu’il faut de l’ordre de 40 questions pour une évaluation de qualité, et dans ce cas l’erreur moyenne sur le score obtenu sera de 1.1 points pour une notation sur 20.
La valeur d'un score obtenu : principes
Une évaluation de connaissances, ou de compétences, vise à estimer le niveau de connaissance d’une personne en lui posant des questions et en analysant ses réponses. Après avoir posé un certain nombre de questions, dont les réponses seront correctes ou erronées, on peut déterminer un score qui va refléter, on l’espère, le niveau de connaissance de la personne.
Dans ce processus, il n’est presque jamais possible de couvrir le domaine de manière exhaustive, c’est-à-dire d’avoir tout demandé et donc tout mesuré. On dit que l’on procède par échantillonnage, c’est-à-dire que l’on considère un sous-ensemble des connaissances du domaine et l’on suppose que les résultats obtenus sur cet échantillon sont représentatifs des résultats qui seraient obtenus sur l’ensemble du domaine.
Mais on sait qu’il existe des facteurs aléatoires qui viennent impacter le score obtenu sur l’échantillon. D’une part l’échantillon a peut-être inclus par chance les sujets que la personne maîtrisait, et peut-être qu’elle connaît moins bien le reste. D'autre part, ne connaissant pas la bonne réponse, la personne a pu répondre au hasard, et avoir la chance de tomber juste.
Si l’on ne procédait pas par échantillonnage, et que l’on posait une infinité de questions, ces aléas disparaîtraient, mais il faudrait pour cela une infinité de temps. Toutefois, en imaginant que cela soit possible, on parviendrait à un score ultime, et ce score serait une représentation parfaite du niveau de connaissance que l’on cherchait à mesurer.
La question qu’il est légitime, et nécessaire, de se poser est : Comment le score obtenu sur un petit échantillon, qu’on appellera Se, se compare-t-il au score ultime, Su ? Le score qui importe c’est Su, celui qui mesurerait le vrai niveau de la personne. Mais on ne le connaît pas et on ne le connaîtra jamais tout à fait. Le score qu’on connaît, c’est Se, celui produit par notre évaluation. À l’issue d’une évaluation, on sera très vite tenté de faire comme si Se était égal à Su, en oubliant que ce n’est pas tout à fait exact, et sans se demander quel est l’écart entre Se et Su.
Or cette question n’est pas sans réponse. On peut même l’étudier de manière très précise, même si c’est un peu mathématique.
Le calcul de fiabilité : explications et exemple
Pour être un petit peu concret, disons que j’ai posé 10 questions à Marie, et qu’elle a eu 7 bonnes réponses. Elle a donc un score de Se de 7/10, ou disons 0.7, ou encore 14/20. En probabilité, on raisonne sur un intervalle de 0 à 1, un événement qui ne peut pas arriver a une probabilité de 0, un événement qui arrivera de manière certaine a une probabilité de 1. Entre les deux, si je joue à pile ou face avec une pièce parfaite, la probabilité d’avoir pile est de 0.5.
Concernant Marie, si son score ultime Su était de 0.5, la probabilité d’avoir juste à chaque question posée serait de 0.5, une chance sur deux.
Je ne connais pas Su, mais, même sans faire trop de maths, je peux dire que si Su était très faible, disons si Su valait 0.1, alors il serait peu probable qu’elle puisse obtenir 7 bonnes réponses sur 10 (ce qui reviendrait à tirer 7 fois sur 10 la boule numéro 1 en piochant dans un sac de 10 boules).
La probabilité d’avoir 7 bonnes réponses sur 10 sachant qu’à chaque question posée elle a une probabilité Pu égale à 0.1 d’avoir une bonne réponse, se calcule comme ceci :
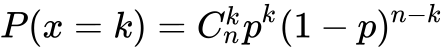
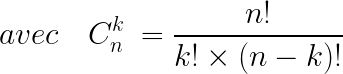
Pour la valeur X = 7, on peut calculer :
P(X = 7) = (10! / (7!(10 - 7)!)) * (0.17) * (0.93)
P(X = 7) = 120 * 0.0000001 * 0.729 = 0.000008748
C’est une probabilité extrêmement faible. Je peux donc dire que je ne connais pas Su de manière certaine, mais que, puisque que Se vaut 0.7, il est très peu probable que Su soit inférieur à 0.1. Autrement dit, si Marie a eu 14/20 en répondant aux 10 questions, il est très peu probable que son score ultime soit inférieur à 2/20. Donc Marie n’est sans doute pas tout à fait nulle, mais on aimerait pouvoir dire un peu mieux que cela. Quelle serait la probabilité que son score ultime soit, disons, 16/20 ?
Je peux faire cet exercice pour toutes les valeurs possibles de Se: pour chacune des valeurs de Su, j’ai une certaine probabilité d’avoir Se = 0.7.
Cette démarche est appelée Inférence Bayésienne, elle consiste à déterminer la probabilité de certaines causes en fonction de la répartition d’événements connus. Ici, la “cause”, c’est le score ultime Su, et l’événement connu c’est le score évalué Se.
Le théorème de Bayes, bien connu des statisticiens, s’écrit comme ceci:
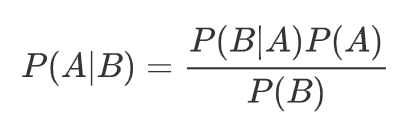
A et B sont des événements potentiellement liés. P(A) est la probabilité de l’événement A, P(B) la probabilité de l’événement B, P(A|B) est la probabilité de A sachant que B est avéré, et réciproquement, P(B|A) la probabilité de B si A est avéré.
Que sait-on de la répartition de probabilité de Su sachant Se ?
Sans entrer dans plus de formules statistiques, la réponse peut se représenter comme ceci:
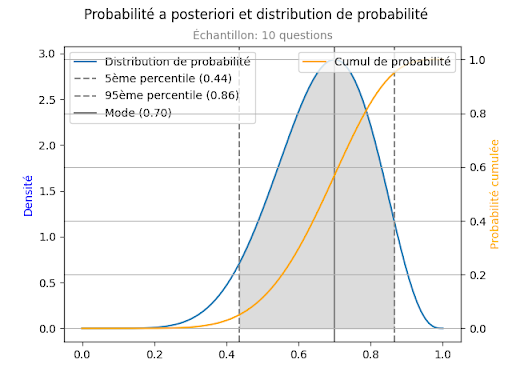
Sur cette figure, la ligne bleue est la distribution de probabilité de Su, sachant que sur un échantillon de 10, on a obtenu une valeur de Se = 0.7. La distribution de probabilité, cela signifie que la probabilité que Su soit inférieure à 0.4 par exemple est la surface sous la courbe bleue (l’intégrale), située entre la valeur 0 et la valeur 0.4 de l’axe des X.
On voit que la courbe bleue atteint un maximum à la valeur 0.7, c'est-à-dire que la valeur 0.7 est celle où la densité de probabilité est la plus forte.
Sur la figure, la courbe jaune est l’intégrale de la courbe bleue. Elle utilise l’échelle de droite, qui va de 0 à 1. Elle s’interprète comme ceci : pour une valeur donnée x1 sur l’axe des abscisses, on lit sur l’axe des ordonnées la valeur de la probabilité pour que Su soit inférieur à x1. Par exemple pour la valeur x1 = 0.7, je vois que j’ai une probabilité de 0.52 pour que Su soit inférieur à 0.7, et donc de 0.48 pour que Su soit supérieur à 0.7.
La courbe nous montre aussi que j’ai une probabilité de 0.05 (5 chances sur 100) pour que Su soit inférieur à 0.44, et de même une probabilité de 0.05 pour que Su soit supérieur à 0.86. Cet intervalle de [0.44, 0.86] est l’intervalle de confiance à 90%. Je peux affirmer qu’il y a une probabilité de 90% pour que Su soit compris entre 0.44 et 0.86. C’est l’intervalle qui est représenté en grisé sur la figure.
C’est à cela que nous voulions arriver: Marie a obtenu une note de 0.7, ou disons 14 sur 20, mais je peux seulement affirmer avec une certitude de 90% que le niveau de connaissance de Marie se situe entre 8.8 et 17.2. C’est un intervalle très large, immense ! Supposons que cette évaluation détermine si un étudiant est admis dans le niveau supérieur, et que le niveau exigé ait été de 15 sur 20. Marie a donc échoué son examen, elle devra redoubler son année. Pourtant, la probabilité que la connaissance réelle de Marie soit meilleure que 15/20 est d’environ 30%. Autrement dit, on a 30% de chances d’avoir recalé Marie de manière injuste. N’est-ce pas choquant ?
Comment réduire le risque d’erreur ? Comment réduire l’écart entre Su, le score ultime, le score véritable, et Se, le score observé ?
C’est très simple, il suffit de poser davantage de questions. Refaisons l’exercice avec 20 questions, et donc 14 bonnes réponses. Le score observé est toujours de 0.7.
On obtient la courbe suivante:
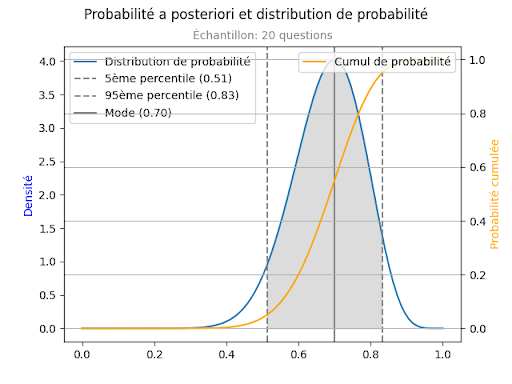
On voit que l’intervalle de confiance à 90% s’est réduit, il est maintenant de [0.51, 0.83]. La probabilité de recaler Marie de manière injuste s’est réduite, elle est maintenant d’environ 20%. C’est encore trop.
Voyons maintenant ce qui se passerait si l’on posait 40 questions:
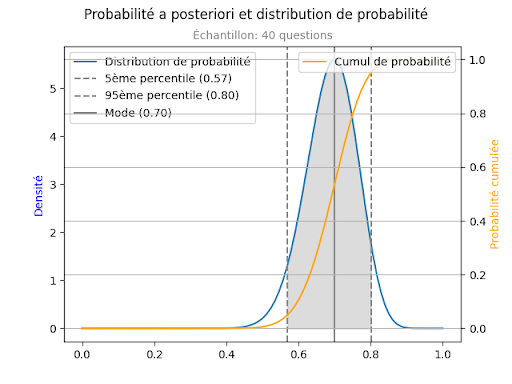
L’intervalle de confiance est de [0.60, 0.78]. La probabilité de se tromper en affirmant que le niveau de connaissance de Marie est inférieur à 15 sur 20 n’est plus que d’environ 10%. C’est peut être encore trop, mais il s’est considérablement réduit.
En synthèse, et avant d’aller plus loin, on obtient confirmation de ce que l’on pouvait imaginer déjà: plus on pose de questions, plus l’intervalle de confiance se resserre. Mais on a pu aussi quantifier cette affirmation, et la conclusion est importante: il faut au minimum une quarantaine de questions pour obtenir un score valable, un score sur lequel on puisse envisager de s’appuyer.
Du coup, on peut se poser une autre question. Nous avons fait le calcul pour 10 questions, pour 20 questions, pour 40 questions. D’une manière plus générale, comment l’intervalle de confiance évolue-t-il en fonction de la taille de l’échantillon, c'est-à-dire pour nous, du nombre de questions posées.
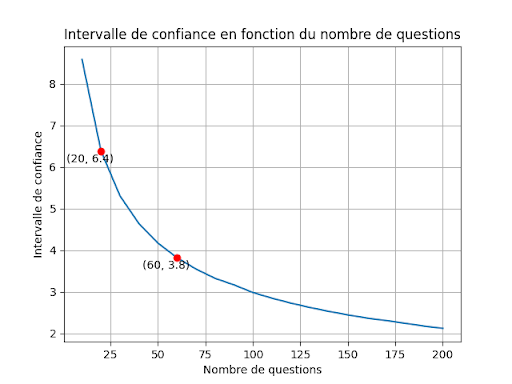
Sur la courbe suivante, on a représenté la largeur de l’intervalle de confiance à 90%, pour une notation sur une échelle de 0 à 20. Par exemple, pour une taille d’échantillon de 60 questions, la largeur de l’intervalle de confiance est de 3.8. On pourrait dire qu’une note est valable à plus ou moins 1.9 (la moitié de 3.8). C’est-à-dire qu' une note de 14 sur 20, peut être interprétée comme: “On est sûr à 90% que la note réelle est comprise entre 14 - 1.9 et 14 + 1.9, c’est à dire entre 12.1 et 16.9”. C’est une légère approximation, car pour être précis, l’intervalle de confiance n’est pas exactement centré sur le score relevé. Mais c’est un détail.
Une autre manière encore d’étudier l’évolution de la qualité de la note en fonction de la taille de l’échantillon est de s’intéresser à l’erreur que je fais, en moyenne, lorsque je considère que Se est égal à Su. C’est une grandeur un peu plus pertinente que l’intervalle de confiance, parce qu’elle intègre le fait que, à l’intérieur de l’intervalle de confiance, toutes les valeurs n’ont pas la même probabilité, les valeurs proches du score observé Se sont plus probables que celles qui sont proches des limites de l’intervalle.
En probabilité, on parle d’espérance. L’espérance est la somme des valeurs possibles, chacune multipliée par sa probabilité d’occurrence. C’est une sorte de moyenne pondérée, où le coefficient de pondération est la probabilité d'occurrence. Lorsqu’on est sur une distribution continue, ce sera l’intégrale du produit (erreur à la valeur x) x (probabilité de la valeur x), sur l’intervalle des valeurs.
Dans notre cas, pour chaque valeur du score ultime Si, on considère l’écart entre Su et Se, en valeur absolue. En raisonnant en termes de distribution, la courbe de densité de probabilité nous donne, pour chaque valeur de l’axe des X, la probabilité pour que Su , soit entre x et x + dx. On va donc intégrer abs(x - Se) * densité(x) sur l’intervalle 0, 1.
L’appellation complète serait “erreur absolue moyenne attendue”, mais nous pouvons simplifier en “erreur moyenne”.
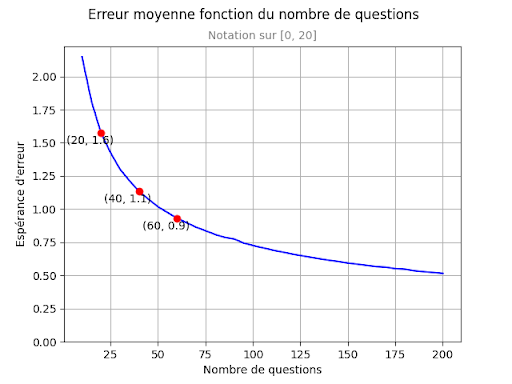
Ici, la grandeur sur l’axe des Y est l’erreur que l’on fera, en moyenne, si l’on utilise le score observé Se comme s’il était le score ultime Su. Comme précédemment, la représentation est pour une échelle de notation de 0 à 20. Et pour un Score observé Se = 14/20.
On a fait apparaître trois points particuliers:
-
Avec 20 questions, la note de 14/20 a une erreur moyenne de 1.6.
-
Avec 40 questions, l’erreur moyenne est de 1.1
-
Avec 60 questions, l’erreur moyenne est de 0.9
On observe que le gain de précision est important lorsque l’on passe de 20 à 40 questions, il est moins important ensuite lorsque l’on passe de 40 à 60 questions. Au-delà de 60 questions, l’amélioration est plus lente encore, et il faudrait poser 200 questions pour réduire l’erreur à 0.5 points sur 20.
On peut exprimer ce résultat de manière simple : il faut au moins 40 questions pour parvenir à un résultat valable, et l’erreur moyenne sera de 1.1 points sur une échelle de 0 à 20.
